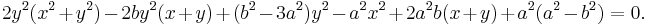Conchoid of Dürer
The conchoid of Dürer, also called Dürer's shell curve, is a variant of a conchoid or plane algebraic curve. It is not a true conchoid.
Contents |
Construction
Let Q and R be points moving on a pair of perpendicular lines which intersect at O in such a way that OQ + OR is constant. On any line QR mark point P at a fixed distance from Q. The locus of the points P is Dürer's conchoid.
Equation
The equation of the conchoid in Cartesian form is
Properties
The curve has two components, asymptotic to the lines 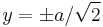 . Each component is a rational curve. If a>b there is a loop, if a=b there is a cusp at (0,a).
. Each component is a rational curve. If a>b there is a loop, if a=b there is a cusp at (0,a).
Special cases include:
- a=0: the line y=0;
- b=0: the line pair
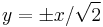 together with the circle
together with the circle 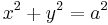 ;
;
History
It was first described by the German painter and mathematician Albrecht Dürer (1471–1528) in his book Underweysung der Messung (S. 38), calling it Ein muschellini.
See also
References
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 157–159. ISBN 0-486-60288-5.